I was recently watching an early X-Files episode called “Conduit” (Season 1 Episode 4). The overall plot doesn’t really matter here, but there is a memorable scene involving a kid who sits in front of a TV displaying static, furiously writing down zeros and ones on paper—line after line.

Mulder notices this strange behavior and suspects these numbers might hold a clue to his mysterious case. He collects some of the pages and sends them off to the “geeks” at headquarters for analysis.
In the next scene, the NSA storms in and takes the kid away! The supposedly random zeros and ones turn out to be binary data containing parts of defense satellite transmissions—highly classified information. The government assumes the boy knows more than he’s letting on.
I won’t spoil the rest of the storyline, but that scene made me wonder how realistic it was. So, I set out to replicate the experiment in my own small way and see if I could discover anything “secret” within random bits.
My Experiment
I started with a blank sheet of printer paper and wrote down a random sequence of 0s and 1s, much like the kid in the episode. On average, I fit 47 bits (0s or 1s) on each line, and I had 46 lines per sheet. That totals 2,162 bits on a single page of paper.
Each 0 or 1 is a “bit.” Bits are quite small, so we usually talk in terms of bytes instead. One byte = 8 bits. Therefore, 2,162 bits equals about 270 bytes (2,162 ÷ 8 ≈ 270.25).
How big is 270 bytes? Not very. If you store text, that’s roughly 270 characters (including spaces and punctuation). It might be about three sentences. For storing integers, we often use 4 or 8 bytes per number, so 270 bytes can store around 67 numbers if we use 4 bytes each. A color image needs 3 bytes per pixel (one byte each for red, green, and blue), so 270 bytes would only give us a 9×9-pixel image—far too small to represent anything meaningful.
Two Key Questions
From here, I wanted to explore two questions:
- If I generate a random 2,162-bit sequence, how likely is it that this exact sequence also appears somewhere in any of the files on my computer? This would tell us how likely it is that the data could uniquely identify a pattern.
- Is 2,162 bits of data enough to store the information the episode claimed? Can 2,162 bits store a defense transmission, a fragment of a classical melody, or part of da Vinci’s Vitruvian Man”?
My initial guesses were:
- This random 2,162-bit pattern would appear often, making it basically impossible to determine its source.
- If we restrict ourselves in certain ways, then yes, 2,162 bits could represent a few of those sample pieces of information (like a short text document, a short MIDI sequence, or a small vector image).
Searching Through Existing Files
Answering the first question is simple in theory: generate 2,162 random bits, then scan every file on my computer—pictures, documents, music, movies, system files, AI models, everything—to see if that sequence appears anywhere in their raw data.
A single MP3 is roughly 4 MiB (mebibytes), which is 33,554,432 bits—about 15,000 times larger than our little 2,162-bit sequence. Movies can run into gigabytes, which is thousands of times bigger. So it felt plausible that somewhere in all those bits, my random pattern might appear by chance.
I wrote a program (it’s quite parallelized) that plowed through every bit of every file on my computer, looking for the exact 2,162-bit pattern. You can see the program here (written in Elixir/Erlang). Execution took a lot longer than I expected, but in the end, the results were…
Not once did the random series of bits appear across a single file!
This was genuinely surprising! In smaller tests (around 200 bits), I had found random patterns appearing multiple times in a much smaller set of files. For reasons that might be statistical or based on how files are encoded, the larger 2,162-bit pattern never showed up in 390 GB of data spanning 1,045,216 files.
So, perhaps The X-Files was onto something. If the data really doesn’t appear in typical large datasets, maybe you could identify the true “source” behind it. That said, you’d still have to compare it across tremendous archives of known data. Given that it took me 40 hours with 16 processors and a solid-state drive to check just one laptop’s worth of data, it seems highly improbable that anyone—especially in 1993—could feasibly run a search at this level across massive datasets.
I suppose if I were more math inclined, I would have skipped out on this whole experiment and just computed the probability. It turns out, that the probability of two sequences of 2,162 bits matching each other in order is 1 in 5.8 × 10650. Winning the Powerball Lottery is only 1 in 2.0 × 109 (2 billion), and being struck by lightning is only 1 in 7.5 × 105 (750,000)! To even have a 0.01% chance of this exact 2,162 bit sequence, we’d need a file with a length of 3.16 × 10648 bits!
That is 3.16 × 10633 petabytes. That is an astronomically large quantity, far exceeding all the data storage capacities conceivable with current or theoretical technology. In fact, it is estimated that the total amount of data stored in the world is about 120 billion petabytes. This number is so far beyond that, it is difficult to compare it to anything!
We do get a slight advantage in that we have a “sliding window” within a continuous sequence of bits. As you can see, in the animation below, if we have a large file with a continuous sequence of bits, we start at the first 2,162, compare them, then slide one bit to the right, and compare the next window of 2,162 bits.
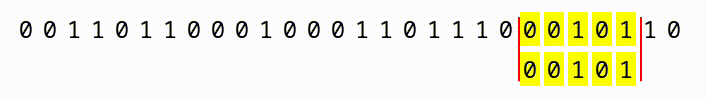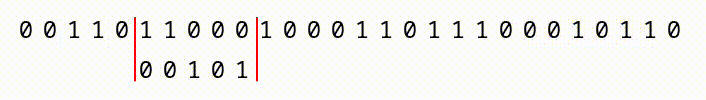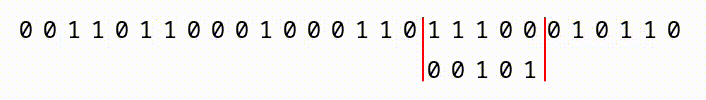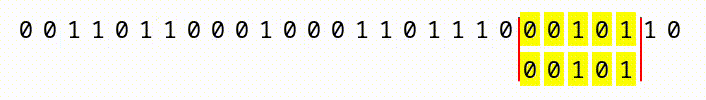
What this means, is that with a file that is 2163 bits long, we’d have two chances for our pattern to match. A 2164 bit long file would have 3 chances, and so on. So, the larger the input files, the more chances we have. But, we’d still have to construct a file so enormous (larger than the whole world’s data collection) that it offers 5.8 × 10650 different positions for the sequence to appear!
Could 2,162 Bits Really Represent “Defense Transmissions,” a Melody, and a Masterpiece?
In the show, the binary patterns are identified as partial snippets of defense transmissions, classical music, and da Vinci’s Vitruvian Man. Let’s see if that’s plausible.
Defense Transmissions
“Defense transmission” can mean many things, but suppose it’s something like:
Secret Military Base 1
ID: xyz
34.180467, -108.292431
Secret Military Base 2
ID: abc
37.542678, -110.055634Names, IDs, and coordinates could fit into 2,162 bits (270 bytes). So yes, you could store one or two base coordinates in that space.
Melody of a Classical Song
Most people think of music as a recorded file—like a CD track. On a CD, audio is uncompressed: 44,100 samples per second, 16 bits per sample, stereo (2 channels). That’s about 1,411,200 bits for just one second of music, way bigger than our 2,162 bits.
But compressed formats exist. MP3 at 192 kbps (kilobits per second) is smaller but still 192,000 bits per second. Our 2,162 bits would cover only about 0.01 seconds of audio—not enough to identify a classical piece by ear.
There are some other ways to record music on a computer. Instead of capturing real world data from a microphone, you can use computer generated sounds. Think of how a keyboard would use generated sounds. The most common format is called MIDI. In this format, you specify a computer generated “instrument” and a sequence of notes. Here is an example of what a MIDI file that plays a C Major scale would look like:
(MIDI files are binary (0s and 1s), so you can’t really read them as text. However, it would take a LOT of space to write all the 0s and 1s, so I’ve written this in hexadecimal notation instead)
4D 54 68 64
00 00 00 06
00 00
00 01
00 60
4D 54 72 6B
00 00 00 44
00 90 3C 40
60 80 3C 40
00 90 3E 40
60 80 3E 40
00 90 40 40
60 80 40 40
00 90 41 40
60 80 41 40
00 90 43 40
60 80 43 40
00 90 45 40
60 80 45 40
00 90 47 40
60 80 47 40
00 90 48 40
60 80 48 40
00 FF 2F 00Here’s that same data with some comments to describe what is happen
4D 54 68 64 // "MThd"
00 00 00 06 // Header length = 6 bytes
00 00 // Format 0
00 01 // 1 track
00 60 // 96 ticks per quarter note
4D 54 72 6B // "MTrk"
00 00 00 44 // Track length: 68 bytes (we’ll explain below)
-- Note for C4 (MIDI 60, 0x3C) --
00 90 3C 40 // Delta=0, Note On, note 0x3C, velocity 0x40
60 80 3C 40 // Delta=96 (0x60), Note Off, note 0x3C, velocity 0x40
-- Note for D4 (MIDI 62, 0x3E) --
00 90 3E 40 // Delta=0, Note On, note 0x3E, velocity 0x40
60 80 3E 40 // Delta=96, Note Off, note 0x3E, velocity 0x40
-- Note for E4 (MIDI 64, 0x40) --
00 90 40 40 // Delta=0, Note On, note 0x40, velocity 0x40
60 80 40 40 // Delta=96, Note Off, note 0x40, velocity 0x40
-- Note for F4 (MIDI 65, 0x41) --
00 90 41 40 // Delta=0, Note On, note 0x41, velocity 0x40
60 80 41 40 // Delta=96, Note Off, note 0x41, velocity 0x40
-- Note for G4 (MIDI 67, 0x43) --
00 90 43 40 // Delta=0, Note On, note 0x43, velocity 0x40
60 80 43 40 // Delta=96, Note Off, note 0x43, velocity 0x40
-- Note for A4 (MIDI 69, 0x45) --
00 90 45 40 // Delta=0, Note On, note 0x45, velocity 0x40
60 80 45 40 // Delta=96, Note Off, note 0x45, velocity 0x40
-- Note for B4 (MIDI 71, 0x47) --
00 90 47 40 // Delta=0, Note On, note 0x47, velocity 0x40
60 80 47 40 // Delta=96, Note Off, note 0x47, velocity 0x40
-- Note for C5 (MIDI 72, 0x48) --
00 90 48 40 // Delta=0, Note On, note 0x48, velocity 0x40
60 80 48 40 // Delta=96, Note Off, note 0x48, velocity 0x40
-- End of Track --
00 FF 2F 00 // Delta=0, Meta Event (End of Track)(Download this MIDI file to hear it)
The MIDI file above would be only 720 bits (90 bytes). That easily fits in our 2,162 bits! So, storing a brief melody as a MIDI file is indeed possible.
da Vinci’s Vitruvian Man
A typical uncompressed “raster” image would require a color value for every pixel. At 3 bytes per pixel, 2,162 bits (270 bytes) yields only a 9×9 image—too tiny to depict anything recognizable. We have some really neat compression algorithms, like JPEG, that might be able to get pretty small, but probably not down to 2,162 bits
Instead of describing an image by specifying a color for every pixel, we can instead describe an image by shapes. Vector graphics store images as shapes, lines, curves, etc. A simplified vector drawing of the Vitruvian Man might fit into a few hundred bytes, depending on how it’s encoded. It’s not as detailed as a full-color photo, but you could theoretically squeeze in a basic line-drawing version.
A vector format might look something like the following:
CIRCLE,BLUE,30,250x34This tells us to draw a circle with a radius of 30 and its center point at 250×34. Oh, and fill it in with the color blue. This will use much less data than having to specify the color of every single pixel!
I happened to search the web and found a vector image of the Vitruvian Man. A simplified vector drawing could potentially fit in our allotted space!
The Realistic Takeaway
From my random-data experiment, it turned out that my 2,162-bit sequence did not appear even once in 390 GB of data. That suggests if you did find that exact pattern in a large dataset, you might be able to trace its source or guess its purpose. On the other hand, analyzing only 2,162 bits to say, “This is partial data from a classical song or a list of government bases,” is still incredibly difficult—especially if any bits are missing or out of order.
If you’re missing even a single leading bit, all the subsequent data shifts and becomes gibberish. Without headers or metadata, you may never figure out the file format. So the show’s premise—identifying partial data as defense transmissions, a melody, and a famous image—is a stretch, but at least it chose examples that could feasibly fit into a single sheet of binary scribbles!
While the X-Files scenario isn’t entirely realistic, it’s still fun that they picked data snippets (text, MIDI, vector images) small enough to work on a single page of handwritten bits. And that, in my opinion, is pretty cool!